2021年PSLE数学考试结束后，不少学生走出考场向家长哭诉，说题目太难，甚至有一题根本做不了！越来越多家长了解情况后，不少人甚至投诉到教育部门，质疑出题的合理性．教育部门首次向社会公开这道“做不了的题”表示完全能做，吸引了各界社会名流纷纷尝试，却难倒了更多人...有多难？先看原题：PSLE 2021 Q5: Helen and Ivan have the same total number of coins. Helen has a numberof fifty-cent coins and 64 twenty-cent coins. The total mass of her coins is1.134 kg. Ivan has a number of fifty-cent coins and 104 twenty-cent coins.(a) Who has more money in coins? How muchmore?(b) Each fifty-cent coin is 2.7g heavierthan each twenty-cent coin. What is the total mass of Ivan's coins in kg?题中不仅涉及到硬币数量、硬币价值，还涉及到硬币质量，信息量很大，多数学生读完题后毫无头绪．少数学生理解题意，提炼条件后看到问题（a）求价值之差，也果断放弃了．一招教你解决此题！
为了更直观地表现两人所持硬币的相同部分与不同部分，笔者用线段图表示：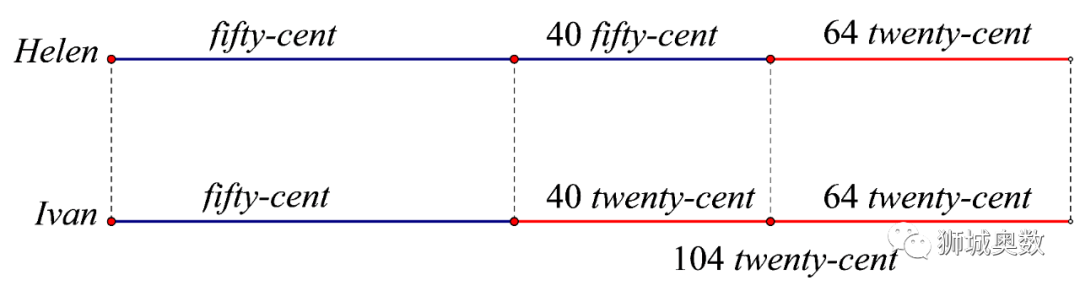
图中，蓝色线段为50分硬币，红色线段为20分硬币，为了求出价值差，我们把两人的相同部分对齐．比较两条线段，由于两人所持硬币总数相同，所以对齐相同部分之后，把相同部分去除，相当于海伦有40个50分的硬币，伊万有40个20分的硬币．所以问题（a）答案：海伦的硬币价值更高，比伊万多了（50－20）×40＝1200（分）．对于问题（b），每个50分硬币比20分硬币重2.7克，则海伦的硬币比伊万要重2.7×40＝108克，即0.108千克，所以伊万的硬币重量：1.134－0.108＝1.026（千克）．以上做法中，我们从“差”的实际含义出发，去掉相同部分，只比较不同部分，这招叫“去同存异”！这招有多厉害？下面我们用这招解决其他类型的数学难题．一招鲜，吃遍天！给大家举几个例子：例1：开心小学的老师为“防尘降霾”植树活动买来一些树苗．这些树苗若第一天种4棵，计划之后每天比前一天多种3棵，则当某一天剩余树苗不够当天计划时，再种30棵就可以完成任务；若第一天种10棵，计划之后每天比前一天多种3棵，当剩余树苗不够当天计划时，再种4棵也可以完成任务，则开心小学的老师一共为这次活动购买了多少棵树苗？分析题意，列举两次种树的情况．第1次：4，7，10，13，...，a，30，其中从4到a是等差数列；第2次：10，13，16，...，b，4，其中从10到b是等差数列．联系两次种树的纽带是树苗总数相等．而通过观察两次种树的情况，我们惊奇地发现，两次种树情况虽然看起来不太一样，但是其中有一部分是完全相同的！如果把第2次的10与第1次的10对齐，并且从总数角度出发可得b大于a，我们就可以把两次种树过程中相同的部分找出来，即10到a这一部分．列成表格：为了更加直观，我们把第1次前面的4和7都加到最后的30上：去掉相同部分，比较不同部分，可以得到结论：第二次种树，在种完a颗后，肯定也种了41棵树．由题意，a大于等于28（否则30棵树就够当天计划了），说明b肯定大于28，由此说明多出来的41棵树肯定无法再种2天，于是b＋4＝41，b＝37．树苗总数为：10＋13＋16＋...＋37＋4＝239（棵）．去同，存异，我们巧妙地求出了第二次种树最后种的棵树情况．
9 条回复
-
曹老师 楼主#1
我们再看一个工程问题：例2：猴子、一起上山摘桃子，猴子单独摘完需要50天，如果猴子第一天摘，猴子第二天摘，这样交替摘，恰好整天数可摘完．如果猴子第一天摘，猴子第二天摘，这样交替摘，恰好比上次轮流的方法多用半天摘完，那么猴子单独摘完需要多少天？分析题意，先列举猴子先摘的情况下，每天摘桃的猴子情况为：，，，，，，...，？再列举猴子先摘的情况下，每天摘桃的猴子情况为：，，，，，，...，？这里需要分析一下，第一种情况中，恰好整天数可摘完到底是最后一天摘还是最后一天摘．如果第一种情况中结尾，说明摘完所有桃子需要若干组，则每组把和互换可知第二种情况也是相同多组的就能摘完所有桃子，天数应当相同！但是条件中天数不同，所以第一种情况中应当结尾．那么我们可以把两次摘桃情况列举如下：去掉前面若干组相同的，比较结尾不同的部分，可以得到结论：最后摘1天相当于摘1天加摘0.5天．这说明摘1天相当于摘0.5天，也即摘2天相当于摘1天．题中，猴子单独摘完需要50天，所以猴子单独摘完需要25天．去同，存异，我们巧妙地得到了猴子和摘桃效率的2倍关系．
-
曹老师 楼主#2
你学会了吗？为了方便同学们自我检验是否学会了“去同存异”，我们给大家准备了几道题目：
做完后大家可以回复或者私信我答案。 -
#3
做补习老师不容易，这么多华语字让接受英文教育孩子真是挑战，反正我家老二看不懂
-
#4
原本就是用来拉开分数的题，一大部分孩子做不出，不也正常，这还是建立在补习成风的现状下的。
So不要用抓狂的文字来制造焦虑。 -
#5
每年都有些人抱怨的，要是人人会做，那还要考试干嘛？怕输也就罢了，还去报纸投诉，把自己孩子不会做的事到处宣扬，也是无法理解啊。我孩子要是不会做，我也是悄咪咪地不出声。
-
#6
Psle明天放榜了，6年没补习，看看我家老二数学拿几分?
-
#7
1. 新加坡小学PSLE数学不需要补习，数学补习一般是为了GEP。
2.上面的题目只要真的跟从学校老师的讲课，认真用心理解了，就一定会做，如果在学校认真用心了不理解或不认真用心，补习了也未必理解。因为题型不变，场景一定会变。 -
#8
PSLE我家老二数学拿了L2
-
曹老师 楼主#9
2021年PSLE数学考试结束后，不少学生走出考场向家长哭诉，说题目太难，甚至有一题根本做不了！越来越多家长了解情况后，不少人甚至投诉到教育部门，质疑出题的合理性．教育部门首次向社会公开这道“做不了的题”表示完全能做，吸引了各界社会名流纷纷尝试，却难倒了更多人...有多难？先看原题：PSLE 2021 Q5: Helen and Ivan have the same total number of coins. Helen has a numberof fifty-cent coins and 64 twenty-cent coins. The total mass of her coins is1.134 kg. Ivan has a number of fifty-cent coins and 104 twenty-cent coins.(a) Who has more money in coins? How muchmore?(b) Each fifty-cent coin is 2.7g heavierthan each twenty-cent coin. What is the total mass of Ivan's coins in kg?题中不仅涉及到硬币数量、硬币价值，还涉及到硬币质量，信息量很大，多数学生读完题后毫无头绪．少数学生理解题意，提炼条件后看到问题（a）求价值之差，也果断放弃了．一招教你解决此题！
为了更直观地表现两人所持硬币的相同部分与不同部分，笔者用线段图表示： 图中，蓝色线段为50分硬币，红色线段为20分硬币，为了求出价值差，我们把两人的相同部分对齐．比较两条线段，由于两人所持硬币总数相同，所以对齐相同部分之后，把相同部分去除，相当于海伦有40个50分的硬币，伊万有40个20分的硬币．所以问题（）答案：海伦的硬币价值更高，比伊万多了（50－20）×40＝1200（分）．对于问题（），每个50分硬币比20分硬币重2.7克，则海伦的硬币比伊万要重2.7×40＝108克，即0.108千克，所以伊万的硬币重量：1.134－0.108＝1.026（千克）．以上做法中，我们从“差”的实际含义出发，去掉相同部分，只比较不同部分，这招叫“去同存异”！这招有多厉害？下面我们用这招解决其他类型的数学难题．一招鲜，吃遍天！给大家举几个例子：例1：开心小学的老师为“防尘降霾”植树活动买来一些树苗．这些树苗若第一天种4棵，计划之后每天比前一天多种3棵，则当某一天剩余树苗不够当天计划时，再种30棵就可以完成任务；若第一天种10棵，计划之后每天比前一天多种3棵，当剩余树苗不够当天计划时，再种4棵也可以完成任务，则开心小学的老师一共为这次活动购买了多少棵树苗？分析题意，列举两次种树的情况．第1次：4，7，10，13，...，，30，其中从4到是等差数列；第2次：10，13，16，...，，4，其中从10到是等差数列．联系两次种树的纽带是树苗总数相等．而通过观察两次种树的情况，我们惊奇地发现，两次种树情况虽然看起来不太一样，但是其中有一部分是完全相同的！如果把第2次的10与第1次的10对齐，并且从总数角度出发可得大于，我们就可以把两次种树过程中相同的部分找出来，即10到这一部分．列成表格：为了更加直观，我们把第1次前面的4和7都加到最后的30上：去掉相同部分，比较不同部分，可以得到结论：第二次种树，在种完颗后，肯定也种了41棵树．由题意，大于等于28（否则30棵树就够当天计划了），说明肯定大于28，由此说明多出来的41棵树肯定无法再种2天，于是＋4＝41，＝37．树苗总数为：10＋13＋16＋...＋37＋4＝239（棵）．去同，存异，我们巧妙地求出了第二次种树最后种的棵树情况．